Available distributions
Risk Analysis supports four distributions. The distribution you choose affects the way in which the selected sampling method - either Monte Carlo or Latin Hypercube - selects a duration for each task for each iteration that is performed during risk analysis.
You specify the distribution that you want to use each time you carry out risk analysis, on the Risk Settings tab of the Risk Analysis dialog. You can also specify that particular distributions should be used with individual tasks. If you apply a specific distribution to a task, this distribution is always used for that particular task when the duration of tasks is determined during risk analysis, regardless of the distribution that you select on the Risk Settings tab of the Risk Analysis dialog.
Uniform distribution
Using this distribution, the selected sampling method takes a random value from within the minimum and maximum duration range that has been specified for each task. If you plotted a graph of hundreds of such random values, the graph would approximate a straight line. The current duration of the task within the project is ignored.
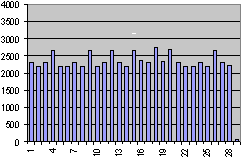
The uniform distribution will provide the most useful results in cases where you know that the duration of tasks will fall somewhere between two values, but you have no feel for the probable duration. This may be the case if someone else has planned a schedule.
Normal distribution
Using this distribution, the selected sampling method takes a random value from within the minimum and maximum duration range that has been specified for each task, tending towards the middle of the duration range. If you plotted a graph of hundreds of such random values, the graph would approximate a normal curve. The current duration of the task within the project is ignored.
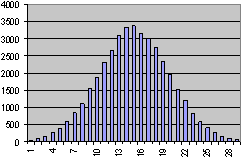
The normal distribution will provide the most useful results in cases where you know that the duration of tasks will fall somewhere between two values and is most likely to fall midway between them.
Skewed normal distribution
Using this distribution, the selected sampling method takes a random value from within the minimum and maximum duration range that has been specified for each task, tending towards the current duration of the task within the project. If you plotted a graph of hundreds of such random values, the graph would approximate a normal curve, but with a peak around the current duration.
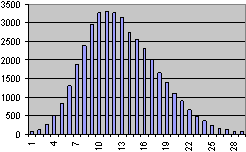
The skewed normal distribution will provide the most useful results in cases where you know that the duration of tasks will fall somewhere between two values and is most likely to fall on the current duration, in other words where you are fairly confident that the current duration of tasks in the schedule is accurate.
Skewed triangular distribution
This distribution produces similar results to the skewed normal distribution. As with the skewed normal distribution, the selected sampling method takes a random value from within the minimum and maximum duration range that has been specified for each task, tending towards the current duration of the task within the project. If you plotted a graph of hundreds of such random values, the graph would approximate a triangle, with its apex around the current duration.
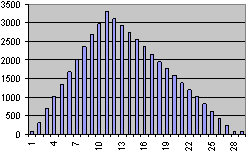
As with the skewed normal distribution, the skewed triangular distribution will provide the most useful results when you are fairly confident that the current duration of tasks in the schedule is accurate.
Estimating the duration uncertainty and probability of tasks