Using logical paths to monitor the erosion of total float
As a project progresses, some tasks will be completed earlier than planned. This increases the total float of any successor tasks. Other tasks will be completed later than planned. This decreases - or erodes - the total float of any successor tasks. If enough non-critical tasks are completed later than planned, their successor tasks will become critical and will impact on the planned finish date of the project.
It can be useful to monitor the erosion of total float, as this enables you to take preventative action before the planned finish date of a project is delayed. One way of doing this is by using "logical paths" to analyse paths of tasks that are not critical, but that may become critical if predecessor activities are delayed, or take longer than planned. Asta Powerproject identifies the various logical paths in a project when you reschedule it. It breaks down the planning data into paths of tasks that are connected by logic links, and orders these paths by the amount of total float contained within them. Each task is assigned a logical path number that identifies the logical path to which it belongs. Tasks with lower logical path numbers are those on logical paths that contain the least amount of total float; the higher the logical path number, the more total float in the logical path. You may find it useful to monitor tasks that are on low-numbered logical paths, as these tasks are more likely to affect the project finish date if they are delayed. Tasks are also assigned a logical path order that defines the order of a task on the logical path on which it is located. The first task on a logical path has a logical path order of 1; the next has an order of 2; and so on.
Asta Powerproject also calculates the duration of the logical path on which a task is located. You may find it useful to compare the total float of tasks against the duration of the logical paths on which they are located, to ascertain which of the tasks on a particular logical path are most likely to affect the project finish date (ie those with the least total float).
Logical paths are identified according to the following rules:
- All tasks without any outgoing links are gathered together into a set of "end nodes" and sorted in ascending order according to their potential impact on the finish date of the project. The end nodes are sorted according to the following criteria, in the following order:
- Task lowest total float.
- Task greatest early finish date.
- Unique task ID.
- Internal task ID.
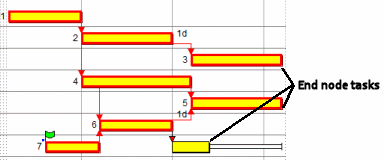
- From the end node task that has the greatest potential impact on the project finish date, the driving predecessor links are followed backwards, each time selecting the link with the greatest potential impact on the finish date of the project. The links are chosen according to the following criteria, in the following order:
- Link lowest total float.
- Whether the link is driving (driving links are processed first).
- Predecessor task lowest total float, then task lowest free float.
- Predecessor task greatest early finish.
- Predecessor task unique task ID.
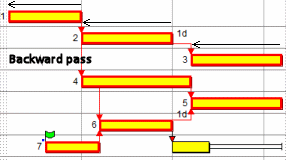
- Once a task with no predecessors (or with only predecessors that have either been visited already or are linked using non-driving links) is reached, the logical path calculation begins with this task. This would be the task on bar 1 in the above illustration.
- From this task, the outgoing links that have the most importance to the finish date of the project are followed forwards, and placed on the same logical path. If a task has multiple incoming links when it is visited, the predecessor tasks at the other end of these links are added to the list of end nodes. These will be evaluated later. The task on bar 6 in the following illustration would be added as a new end node task:
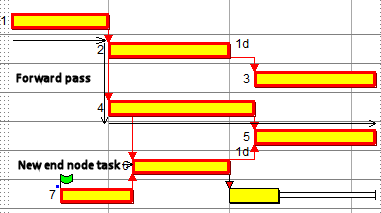
- Once a task with no driving links (or no outgoing links at all), or a task with a greater amount of total float (meaning it is less "critical") is reached, the logical path stops and Asta Powerproject assigns a number to it. The number 1 is assigned to the first logical path and this number is incremented by 1 for each subsequent logical path.
- If the logical path has stopped at a different task to the one at which the process started in step 2, steps 2 to 5 are followed once more, starting again from the task at which the process started in step 2. This process is repeated as many times as necessary until the logical path being followed stops at the task at which the process started.
- Once the logical path being followed stops at the task at which the process started, all logical paths leading backwards from this task have been explored. The remaining end nodes are re-sorted according to the criteria listed in step 1, then the logical path calculation starts again, beginning at the next end node.
- When the paths leading backwards from all end nodes have been explored, the process is complete.
Hammocks are always assigned a logical path number of zero. The same is true of summary and expanded tasks, even if they have incoming or outgoing links. Completed tasks have no effective logic and are therefore ignored. If a bar contains more than one task, the implied links between the various tasks on the bar are treated as logic links.
How summary and expanded task links affect logical path calculations
In Asta Powerproject, you can link to and from summary tasks and expanded tasks, which introduces additional implied predecessors and successors. For example, linking to the start of a summary task is equivalent to linking to the start of each task in the summary group - even though only the earliest task(s) in the summary group will actually be constrained by the link.
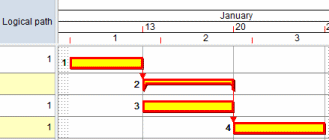
These implied links are taken into account when calculating logical paths. This means that if tasks that are on a particular logical path link to and from a summary task, the most critical tasks in the summary group will be included in the logical path. This is illustrated below, where the tasks on bars 1 and 4, which are on logical path 1, link to and from a summary task; the task within the summary group is included in logical path 1:
Asta Powerproject calculates the logical path duration by summing the duration of the tasks in each logical path. If a logical path contains only Finish-to-Start links with no lead/lag, the logical path duration is the sum of the duration of the tasks on the path. If a logical path contains links of other types, or links that have lead/lag, this will affect the logical path duration, as illustrated below.
In the following example, the sum of the duration of the tasks in the logical path is 7d. However, the logical path duration is 9d, as one of the logic links has 2d lead/lag, which increases the duration of the path:
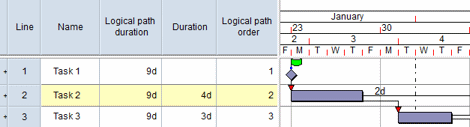
In the following example, the sum of the duration of the tasks in the logical path is 11d. However, the logical path duration is 8d, as the positioning of the links means that only 1d of task 2 is included in the path's duration:
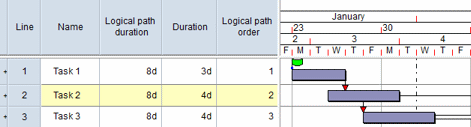
In the following example, the sum of the duration of the tasks in the logical path is 7d. However, the logical path duration is 4d, as the Finish-to-Finish link means that task 2 contributes nothing towards the logical path duration:
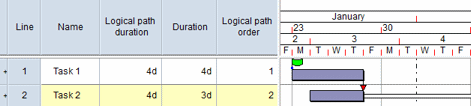
In the following - rare - example, the sum of the duration of the tasks in the logical path is 7d. However, the logical path duration is -3d, as the Start-to-Finish link causes the logical path to flow backwards rather than forwards:
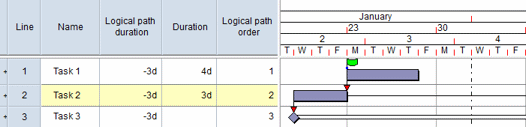
Sorting/grouping by logical path
You may find it useful to create sort/groups in which tasks are sorted/grouped first by logical path and then by logical path order, as this displays logical paths in the clearest possible way. Sorting/grouping a view in this way is a good idea if you are planning to analyse the view as a PERT chart in Network Viewer, as it results in PERT charts that are laid out in the clearest possible way.
You can also sort/group tasks by logical path duration. Logical path duration can be seen as a measure of the importance of logical paths: longer logical paths have a broader scope of activities than shorter logical paths and therefore have much scope to affect the project finish date.
Filtering by logical path
You can filter for tasks that are located on specific logical paths. In conjunction with sorting/grouping by logical path and logical path order, filtering for tasks on specific logical paths helps you to monitor tasks on the lowest-numbered logical paths - ie those that are more likely to affect the project finish date if they are delayed.
Spreadsheet fields that help you monitor the erosion of total float
The following spreadsheet fields are useful when monitoring the erosion of total float:
- Logical path.
- Logical path duration.
- Logical path order.
- Total float variance. This displays the difference between the total float of a task in the live data and its total float in a particular baseline. Once you have identified those tasks that are most likely to affect the project finish date if they are delayed, you can monitor the total float variance of these tasks to ascertain whether it is increasing or decreasing as a project progresses.
If you open the same project in Asta Powerproject and Primavera software and calculate logical paths in each, you may notice that some tasks appear on different logical paths. This is caused by the following Primavera behaviour, which differs from Asta Powerproject:
- Primavera software treats all outgoing links from tasks that are constrained to be as late as possible as driving links; in Asta Powerproject such links are treated as driving links only if the task was already critical according to link logic.
- In Primavera software, the reschedule network includes all tasks; in Asta Powerproject, the links between completed tasks are excluded from the reschedule network. This means that when calculating logical paths in Asta Powerproject, we can never "jump" from one path to another if the earlier tasks are completed.
- Primavera software calculates free float for all tasks, even for those that are critical; Asta Powerproject does not calculate free float for critical tasks. This can cause different results when traversing the task hierarchy in calculating logical paths. This is most obvious where a logical path ends at a task that is constrained by a Start On or Finish On flag: in Asta Powerproject this task has zero total and free float, but in Primavera software it has greater than zero free float.
- When Primavera software re-sorts end node tasks on paths that are not critical, it sometimes orders the end node tasks differently to Asta Powerproject - seemingly illogically.
Calculating the cascade activity number of tasks when rescheduling